By Tim Kirchner

When considering the nature of space-time, it is often useful to start with the equation for relativistic time dilation, since it has been both mathematically derived, and empirically confirmed.

We define our variables as follows:

Then we have the well-known equation

Simple algebraic manipulation of the equation yields

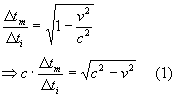
At this point, we make a new definition:

Naturally, since velocity itself is based upon time, this definition for a "velocity in the t-dimension" is more mathematical than it is intuitive. (However, since all things may only be expressed relative to each other, we can think of this velocity as a relative speed compared with motion in the spatial dimensions.)

Henceforth, we will use the following definition as well:

Thus, going back to (1) and substituting, we have

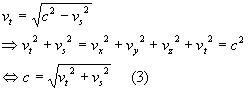
This demonstrates two basic concepts about space-time:

1) all objects have a velocity c in space-time

2) all objects at rest in space have a velocity c in the time dimension

Of course, this is based upon the validity of our initial definition for velocity in the t-dimension. We now must demonstrate the validity of such.

To verify, at least conceptually, that this makes sense, we go back to Einstein’s assertion that the speed of light is constant in a vacuum. It follows from this that the same would hold true for all electromagnetic waves. It is also known that all "particles" also behave like waves. (This has been demonstrated in various experiments such as the two-slit experiment.)

So, given the theory that all things are actually waves (or may be considered such, one way or another), then we have that all things must actually travel at the speed of light. Now, since we have observed objects at rest in spatial dimensions (or at the very least, moving slower than the speed of light), then all of this motion must be in the time dimension, and hence we have a logical basis for equation (3).

Now, there are many results that can be obtained from this.

Since we are considering time to be not unlike a fourth spatial dimension, we can begin to apply the rules of spatial physics as rules of temporal physics. The most important of these rules is the law of the conservation of momentum. We know that this means momentum is conserved in each of the three spatial dimensions. When we extend this to the fourth dimension, time, we get a very powerful result: in all collisions, time is conserved. Logically, we can verify this quite simply: All objects move at a velocity c in space-time, and thus any given object of a mass m has not only a constant mass m and a constant velocity c, but also a constant momentum mc. We know intuitively, then, that since no mass is lost or gained, the momentum in four-space of a system is conserved.

Now we must consider a very unique situation: what happens when mass is lost or gained? First, consider the creation of mass, say an electron and a positron. When created (in gamma rays, for example), the two move away from each other in space, and momentum is conserved. Now, using conservation of space-time, we find that the two should also be moving away from each other in time. That is to say that one particle begins to move forward through time, while the other begins to move backward. Thus, we now have an important property of anti-matter: it moves backwards through time.

A powerful result now falls from this assertion. If we consider the "big bang" to be time t=0, then we have a starting point for v_t. Under the big bang theory, space has expanded as time has elapsed, and at this time, t=0, the total volume of space was zero. Thus, when matter/anti-matter were created, matter entered the universe, and anti-matter couldn’t. (Possibly it went into another universe?) Herein lies the answer to one of the biggest open questions in physics- why the universe is matter dominated.

Going back to the wave-particle duality of things in this universe, we find an interesting characteristic to distinguish the two.