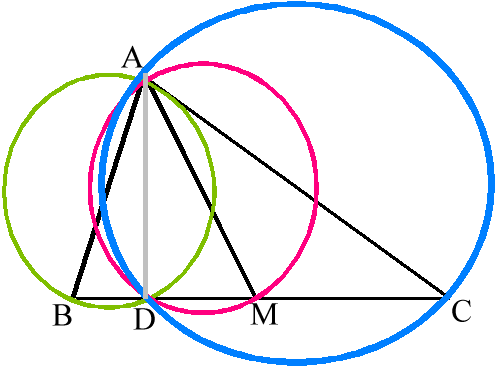
Let ABC be a triangle and D the foot of the altitude from A. Let E and F be on a line passing though D such that AE is perpendicular to BE, AF is perpendicular to CF, and E and F are different from D. Let M and N be the midpoints of the line segments BC and EF, respectively. Prove that AN is perpendicular to NM.

Solution #1 by Tim Kirchner

Let w ₁ be the circle with diameter AB (shown in green), let w ₂ be the circle with diameter AC (shown in blue), and let w ₃ be the circle with diameter AM (shown in red).

AE^ BE Þ EÎ w ₁ and AF^ CF Þ FÎ w ₂

Let l be the line containing D, E, F, and let D,N’Î EFÇ w ₃.

(i.e. since l intersects w ₃ at two points, one is D, call the other one N’)

Since N’Î w ₃, we know that AN’^ MN’.

We are given that N is the midpoint of EF, so it suffices to prove that N’=N, that is to say that N’ is the midpoint of EF.

We now draw in the line l, giving us the following diagram:

Now, Ð ABC and Ð AEF each subtend arc AD of w ₁. Thus Ð ABC = Ð AEF.

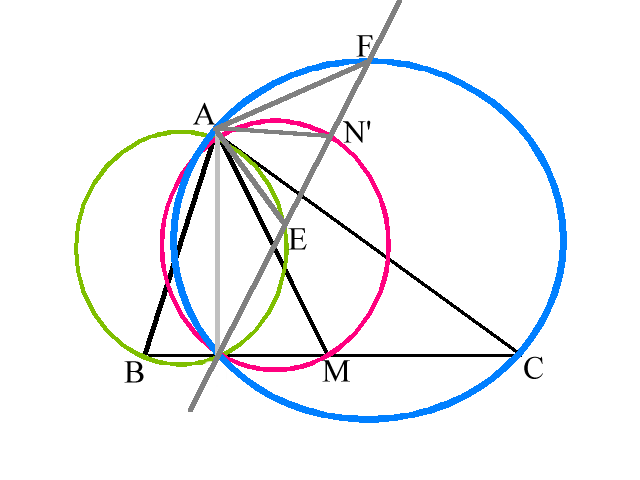
Similarly, Ð ACB and Ð AFE each subtend arc AD of w ₂. Thus Ð ACB = Ð AFE.

Furthermore, Ð AMB and Ð AN’E each subtend arc AD of w ₃. Thus Ð AMB = Ð AN’E.

From this, we know that D ABC ~ D AEF, and D ABM ~ D ABN’.

Thus, since M is the midpoint of BC, N’ is the midpoint of EF.

Therefore, N’ = N.

\ NÎ w ₃ Þ AN^ MN. ÿ